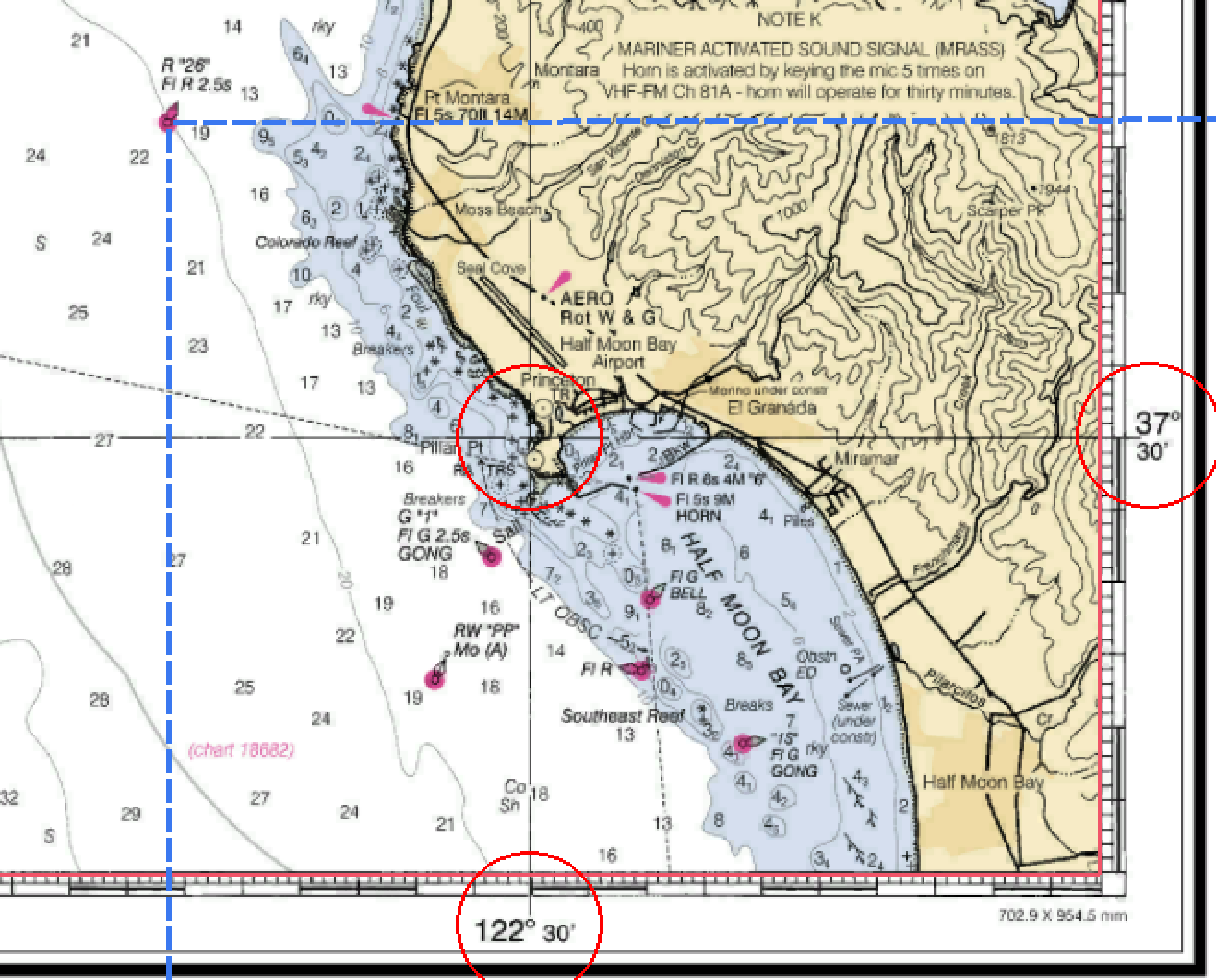
Rose's Intro to Navigation - Navigation in a Modern World

Finding Latitude and Longitude

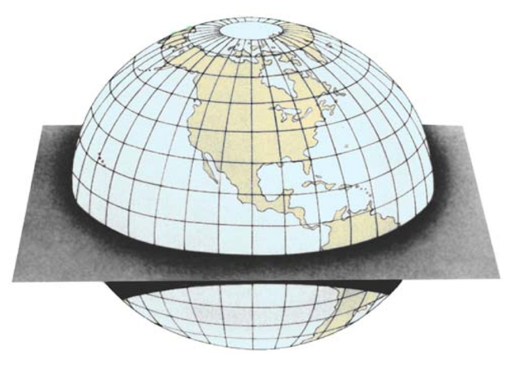
Lines of latitude run east and west (across the chart). Lines of longitude run north and south (up and down).

Degrees of Latitude

Zero degrees of latitude is known as the equator. Latitude goes from zero degrees to 90 degrees north and south of the equator. As can be seen in the image above, Lines of latitude run parallel to each other. There are 60 nautical miles between each degree of latitude. Lines of latitude are a consistent distance apart, so they can be used to measure distance.

One degree of latitude can be divided into 60 “minutes”. Each minute of latitude is one nautical mile.

A minute of latitude can be further divided into 60 seconds. However, it is more common today to divide minutes into tenths and hundredths of a minute. The chart examples below all degrees, minutes, and tens of a minute for both latitude and longitude.

Degrees of Longitude

Zero degrees longitude (also known as the prime meridian) runs through Greenwich England. Longitude goes from zero degrees to 180 degrees east and west of Greenwich England. At the equator lines of longitude are about 60 miles from one degree to the next, however, as can be seen in the image, lines of longitude come together at the poles so they can not be used to measure distance.

A degree of longitude an be divided into 60 minutes and 60 seconds (or into tenths and/or hundredths).

Finding the location of Half Moon Bay

Putting this information together, the latitude and longitude of Half Moon Bay near San Francisco is 37° 30′ N and 122° 30′ W. Which means 37 degrees 30 minutes north of the equator and 122 degrees 30 minutes west of Greenwich England.

First Lat Long Exercise

Use the dashed blue lines to find the latitude and longitude of the buoy named R”26″ Fl R 2.5s.

The Lat and Long of the point north of Half Moon Bay is approximately 37° 30′ N and 122° 30′ W.

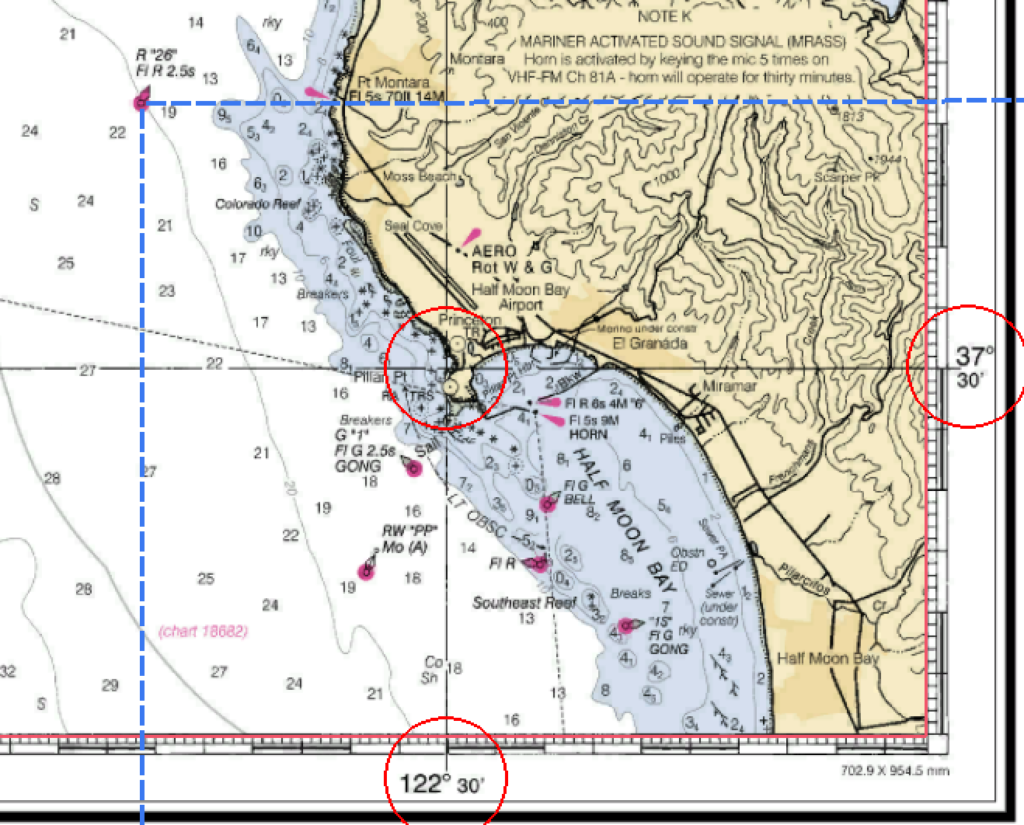
Parallel Rule

One navigation tool you will use a lot is the parallel rule. It is two straight edged “rulers” placed side by side and connected with hinges. These hinges allow you to separate the rulers, moving them further apart, while staying perfectly parallel with each other. Using them, you can “walk” a line from one location on the chart to another, and know that the line is parallel to the original line.

Charts have “major” latitude and longitude lines printed directly on the chart for reference. In the case of the chart image above, latitude 37° 30′ and 122° 30′ have been printed in black on the face of the chart.

To use a parallel rule, line one of the outside edges along a printed line of latitude or a line of longitude. Hold that side rule firmly in place and separate the two rulers, “walking” it up to the object you are concerned with. In the case above, buoy R”26″.

Draw a line from the “object” to the latitude scale to find the latitude of that object.

Repeat the process using a line of longitude to come up with the latitude and longitude of that object.

Finding an Object or Location at a Known Latitude/Longitude

The parallel rule can also be used to find an object or location on the chart when only the latitude and longitude are known.

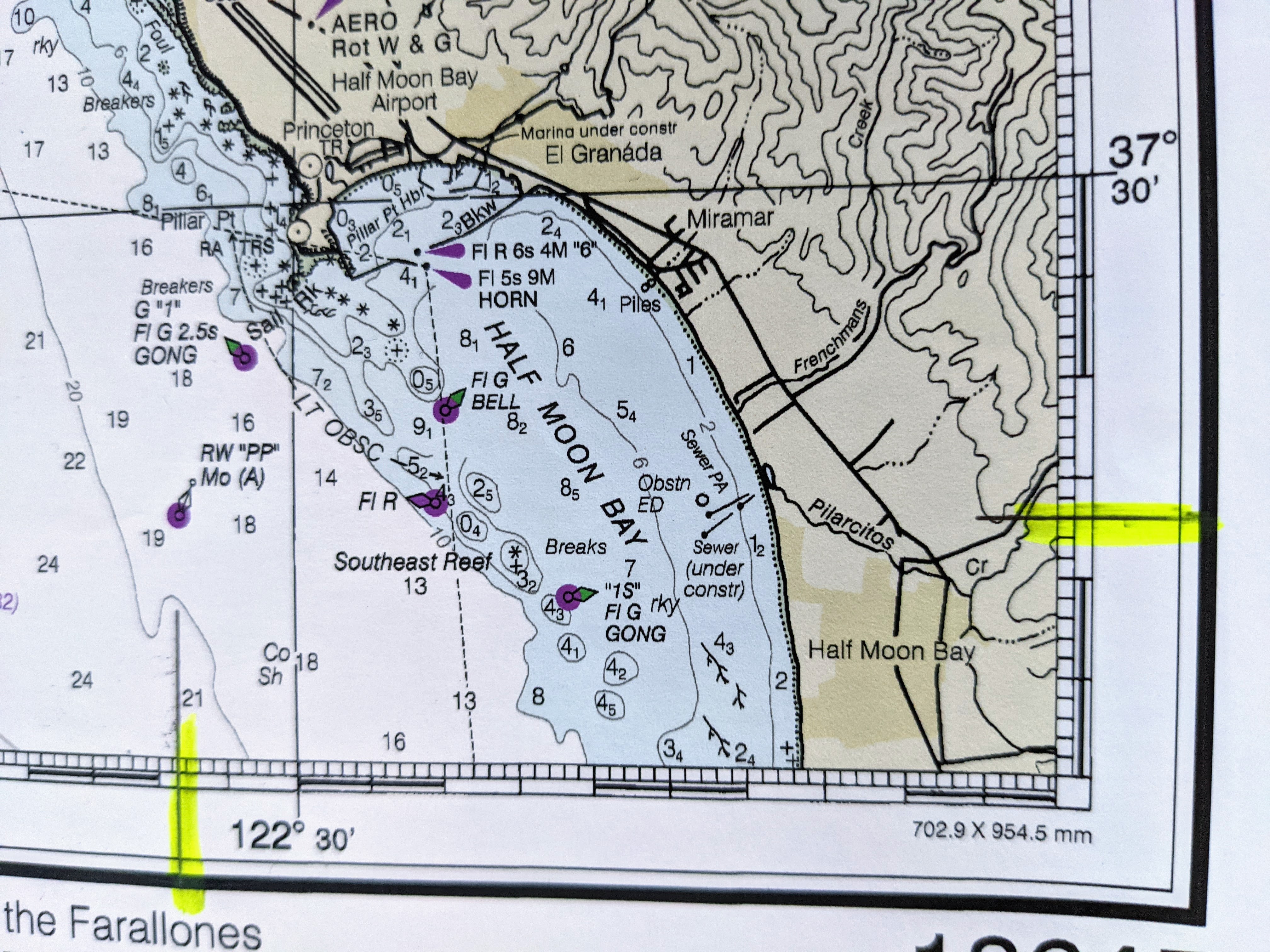
The given latitude and longitude of 37° 28.3′ N and 122° 30.9′ have been highlighted.

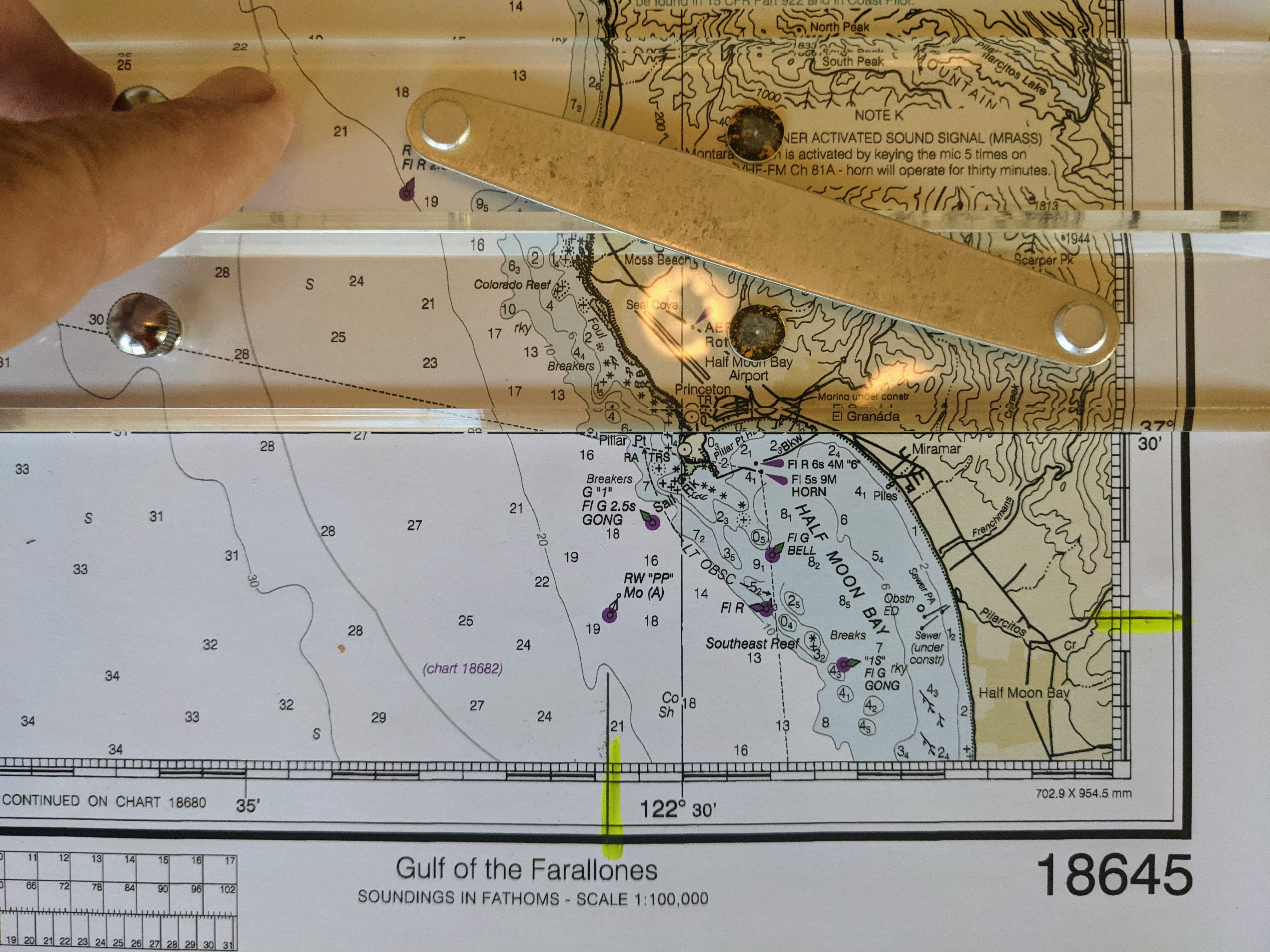
Set up the parallel ruler on the printed latitude line.

Hold one firmly rule in place while the other is moved down the page to line up with the highlighted latitude.

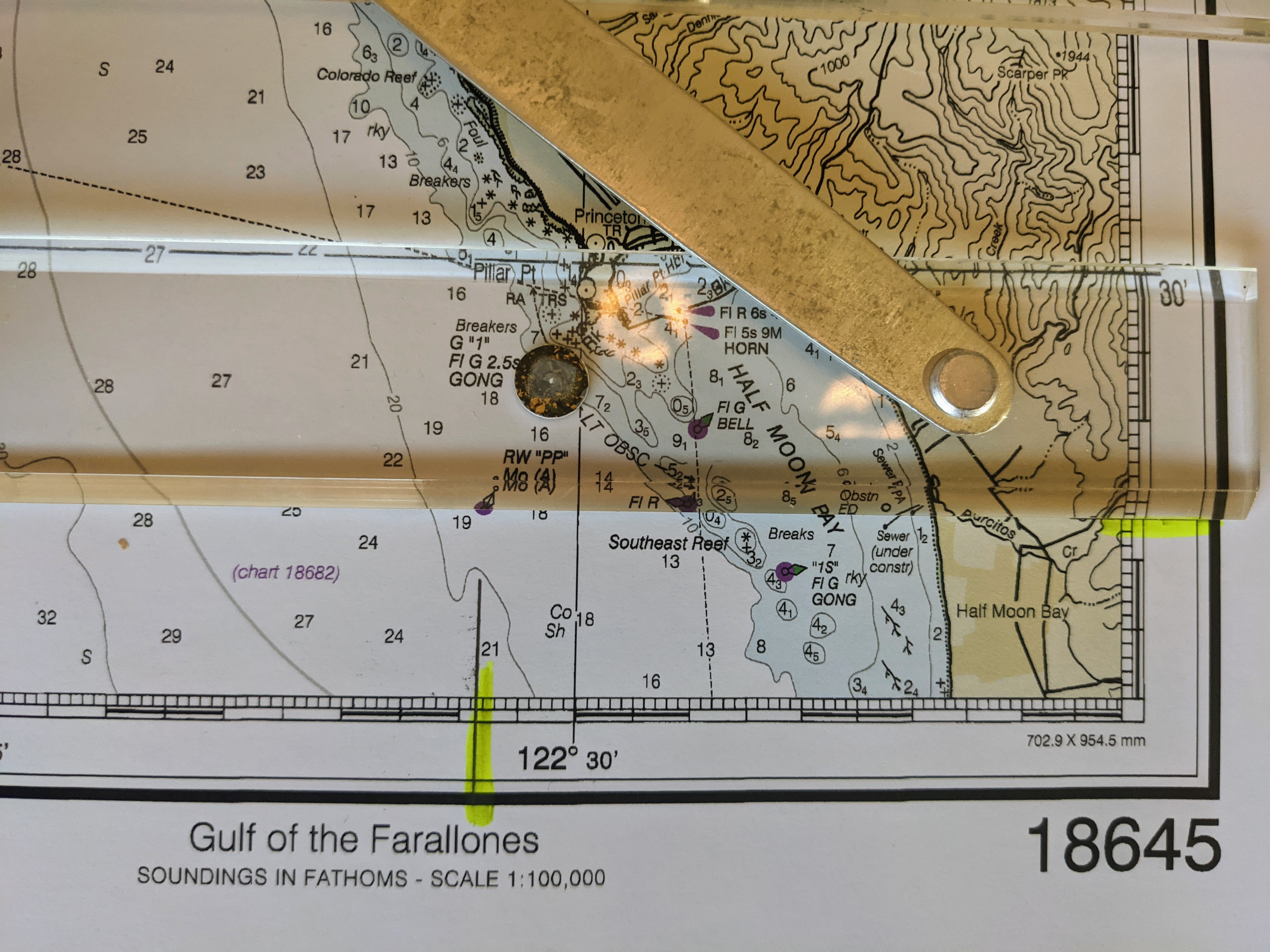
Repeat with a line of longitude and the highlighted longitude. The object, in this case buoy RW”PP” should be found at the intersection of these two lines.

Latitude and Longitude/Parallel Rule Exercise

Download and print the attached portion of chart 18645 for an exercise in finding latitude and longitude.

Finding Objects from Latitude and Longitude

Lat-Long Exercise

1 file(s) 5.97 MB

Download

What is the name of the object at 37° 59.0′ N; 122° 57.3′ W (label it as point “A”)
What is the name of the object at 37° 51.6′ N; 122° 41.7′ W (label it as point “B”)

Finding Course/Direction

Course and/or direction is also found using the parallel rule. Simply lay one edge of the rule from one point to the next and draw a line between the two points. Hold one side of the rule in place and walk the other side to the “+” located in the center of the compass rose. Mark the course.

Lay the parallel rule along the course of travel. In this case, from RW”PP” near Half Moon Bay to the Farallon Islands.

Draw a line along the direction of travel.

Hold one side of the parallel rule in place and move the other side to the small “+” in the center of the nearest compass rose.

Mark the course along the degree scale of the rose.

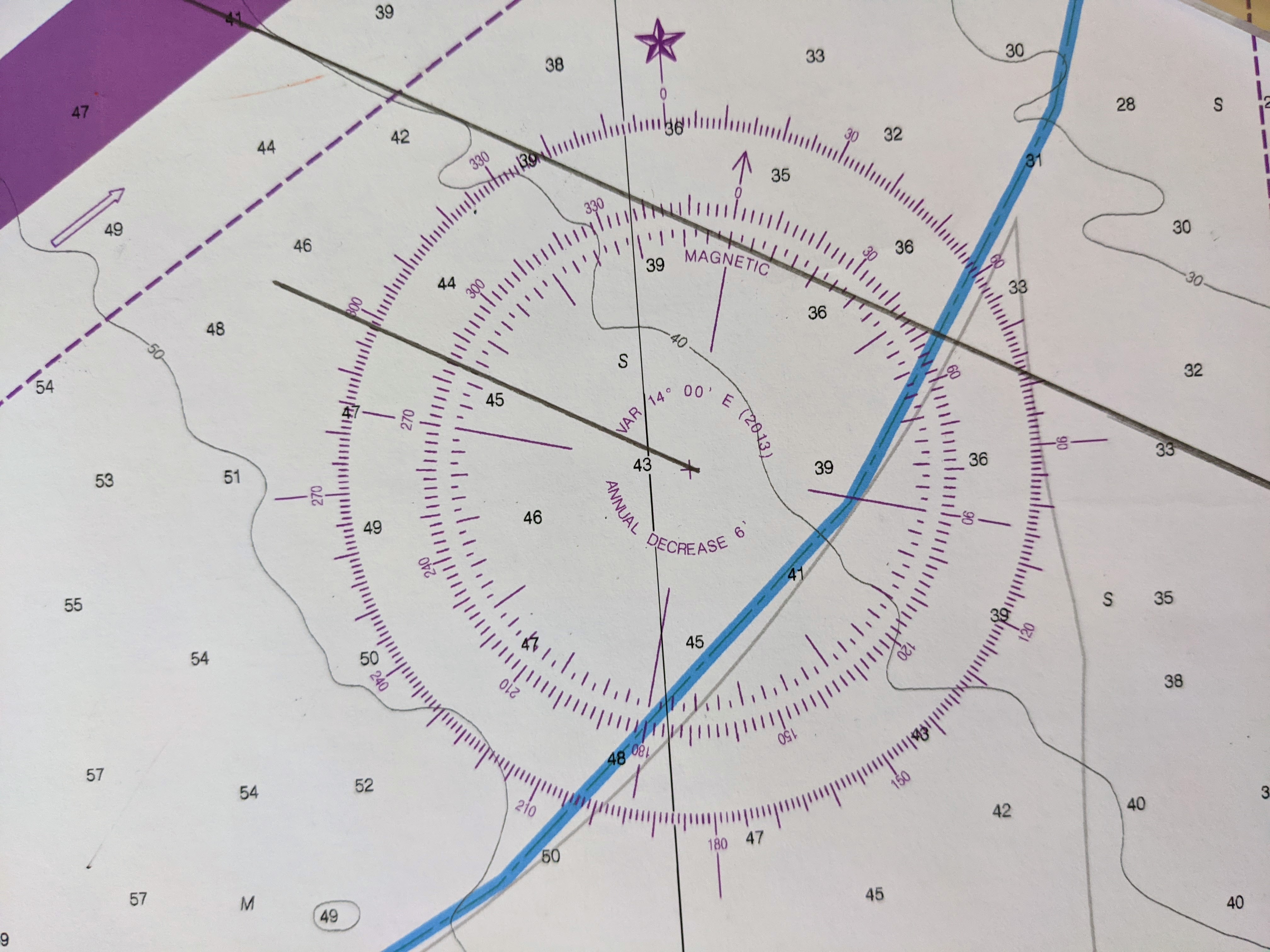
Here is a close up image of the compass rose showing course line and the the degrees both marked. In this case, the course is between 298 and 299 degrees.

Always make sure your course is marked in the same direction from the center of the rose as your direction of travel!

Course Exercise

Use the chart you downloaded and printed earlier.

Assuming that you have found the two buoys, lay one edge of the parallel rule between them. Draw a pencil line.

Now, hold the side of the rule in place that connects the buoys and move the other rule to the small + in the middle of the compass rose. Where the parallel rule “exits” the compass rose is the direction (or course) from one buoy to the other. Caution – if you are traveling from point A to point B, the course will be in the same direction of travel from the + to the outer ring of the compass rose.

What is the course?

Distance

Distance is calculated by comparing the distance between two points with the latitude scale. The easiest way to do this is by using dividers.

The dividers are set to 5 minutes of latitude. Remember, each minute of latitude equals 1 nautical mile.

“Walk” the dividers along the course line. Most likely the last step will be past the end point. Narrow the dividers down to stop at the end point and compare this measurement with the latitude scale. The distance is the combined total of all the “steps” of walking the dividers.

Distance Exercise

What is the distance from Point A to Point B on the downloaded chart?

Distance Speed and Time

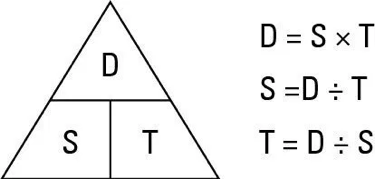
The relationship between Distance Speed and Time is critical in navigation. If you know any two them, the third can be easily calculated.

Distance divided by Speed Equals Time (in hours and tenths of an hour)
Distance divided by Time Equals Speed
Speed multiplied by Time Equals Distance

D Street Triangle

Using the results of the last exercise. If you travel from Point A to Point B you have traveled 14.4 miles. If it took you 3.1 hours (which is 3 hours and 6 minutes) the equation would look like:

14.4/3.1 = 4.6 knots

Let’s take the same situation, but this time assume your boat speed is 6 knots. How long will it take to travel the 14.4 miles?

If you leave at 10:00AM, what is your estimated time of arrival?

Fuel Consumption

GPH

On a boat, fuel consumption is referenced as Gallons Per Hour. Here is a hint for you on fuel consumption calculations. Per always means divided by when used in a math equation.

If you use 3.75 gallons of fuel over a 5 hour period of time. Your GPH is 3.75 / 5 = .75 gallons per hour

Using the same reasoning, GPH times the hours underway equals the total fuel used. .75 GPH for 12 hours equals 9 gallons of fuel used.

F / T = GPH
GPH * T = F
F / GPH = T

If your boat consumes .6 gallons per hour, how much fuel would you use traveling from Point A to Point B in the above example?

If you have a 30 gallon tank and you want to keep a minimum of 25% in reserve, how much usable fuel do you have?

Based on that amount of usable fuel, how long can you motor at .6 GPH?

At a boat speed of 5 knots, how far will you travel during that time?