Category: Radar

Radar for Collision Avoidance
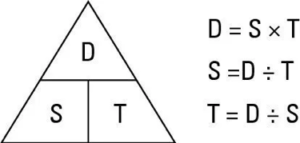
In the CPA – Closest Point of Approach lesson we discussed general plotting concepts of another vessel’s relative movement using Distance and Bearing along various time intervals to derive a solution as to how close the other vessel will approach if your course and speed and their course and speed remain unchanged.

The example used developed an RML between “you” and vessel “M” of 081R, with a CPA of 2 miles at 352R. TCPA was found to be 0948, 48 minutes after point of first contact.

Obviously, there is no risk of collision in this case, however, some additional information may be developed that will be useful.

Related Pages

Closest Point of Approach

Understanding the Maneuvering Board

Downloads

Maneuvering Board PDF

Relative Motion to True Motion

The solution thus far only provides information regarding the relative movement of the other vessel compared to you, not its true course and speed. There are times the true course and speed of the vessel are needed. A vector triangle is the answer.
Head Up vs North Up

At this point it is critical to determine if your display is set to head up or north up. The steps are similar with the different views, however, there are some important differences. This exercise will assume you are operating in head up mode.

Three Vectors Make a Solution
1. Own Ship Course and Speed Vector
2. Relative Motion Course and Speed Vector (RML)
3. Other Ship True Course and Speed Vector
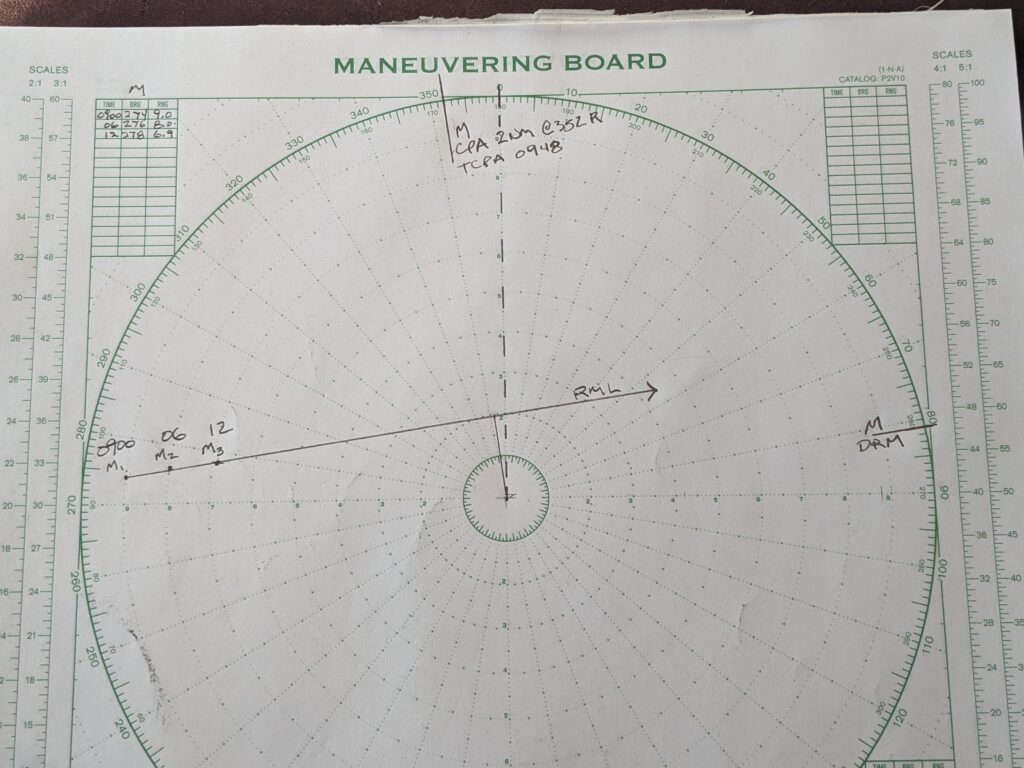
To determine true motion, start by plotting what you know. You know your own course and speed vector, and you know the relative course and speed vector.

Since you want to plot what your vessel did during the time you were tracking the other vessel, begin at point M₁ and plot your course and speed backward in time. Remember that you are in head up mode, meaning you will plot your course backward from your head up course of 000 a distance equal to your speed. Assuming a speed of 5 knots, over a six minute time period, you would travel .5 miles.

Three new labels and three new combinations of those labels need to be introduced at this time.

Own Ship Course and Speed “em”, RML “rm”,
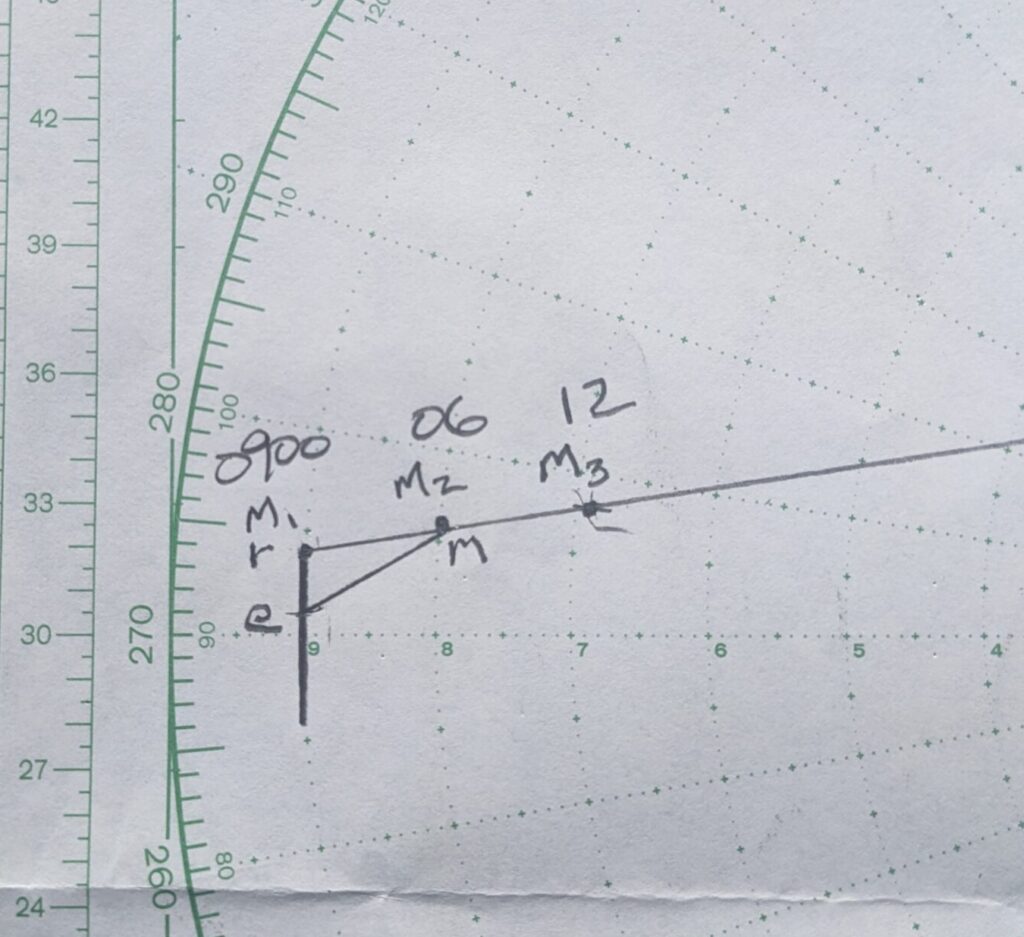
other ship true course and speed “em”
Vector Triangle Plot Labels
- e … The origin of any ship’s true (course-speed) vector; fixed with respect to the earth. This label will represent the origin of your ship’s course and speed as well as the other vessel’s true course and speed.
- r … The end of own ship’s true (course-speed) vector, er; and/or the origin of the relative (DRM-SRM) vector, rm.
- m … The end of other ship’s true (course-speed) vector, em; and/ or the end of the relative (DRM-SRM) vector, rm.
Combining the e, r, and m labels on the plot results in the following vectors.
- er – Own ship’s true (course-speed) vector
- em – Other ship’s true (course-speed) vector
- rm – The relative (DRM-SRM) vector; always in the direction of M₁→ M₂→ M₃ …
Labeling the Vector Triangle

Point M₁ will now also be known as “r”
Point M₂ will now also be known as “m”
The beginning of your course is known as “e”

Line em is the other vessel’s true course (or vessel aspect) and speed. In this case, a bearing 060 @ 12 knots.

Aspect

At its CPA, you should be looking at the starboard “green light” side of the vessel which will be oriented 60^∘ from head on and can be stated at a “green 60^∘” aspect. This becomes important when determining the burdened vessel’s responsibilities.
Course and Speed to Avoid a Passing Vessel

The previous example did not result in a possible collision course or the requirement to maneuver to avoid. Let’s try another now.

Your vessel is on a course of 000^∘ with a speed of 6 knots. The radar is set to head up mode. At 1730 another vessel (M) is observed at 060R with a range of 9 miles. At 1736, the bearing is 060R and the range has reduced to 7.6 miles. Use a mo board to determine the following:
What is the DRM, SRM, CPA, and TCPA?

What is the true course and speed of M?

What is the aspect?

Course to Steer Problem Answers
Assuming you are the burdened vessel, we will calculate a course to steer to allow M to pass 1.5 miles ahead of our ship, with us executing the maneuver at a range of 5 miles.
New Relative Motion Line (NRML)

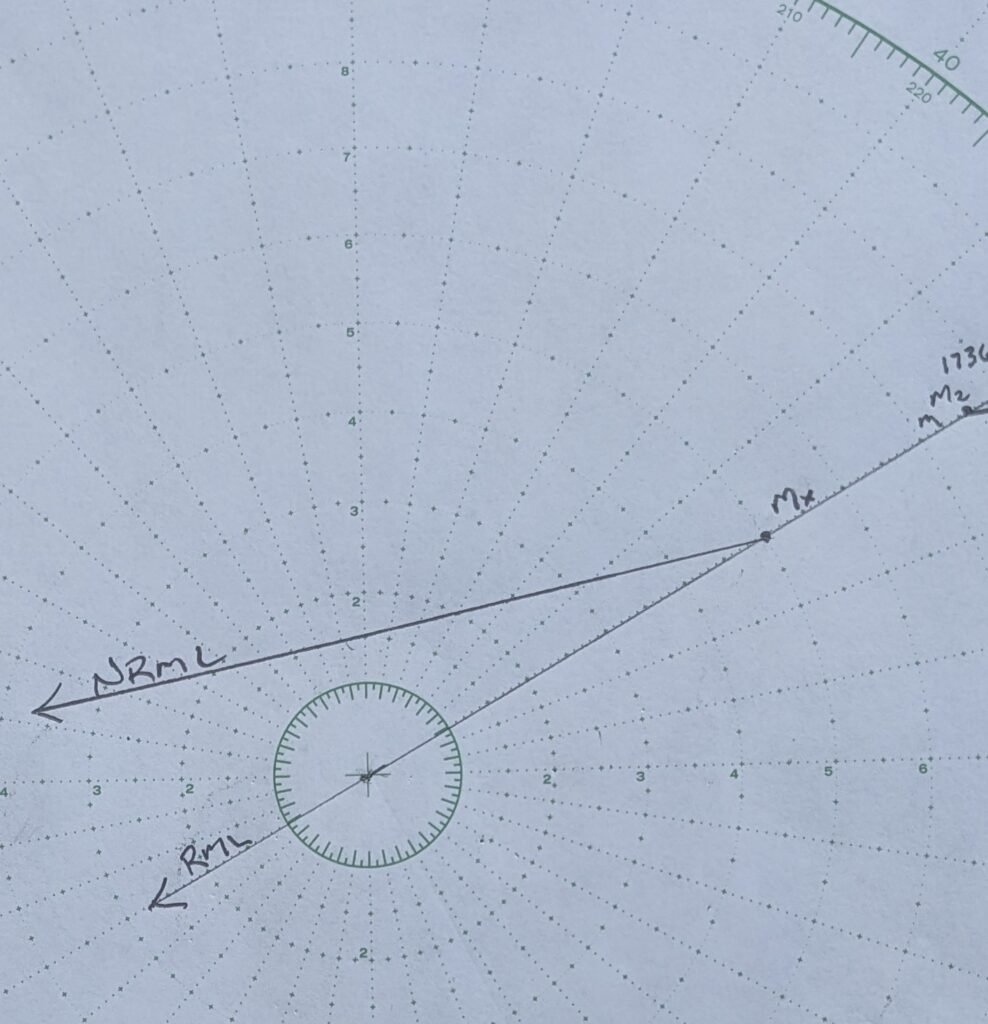
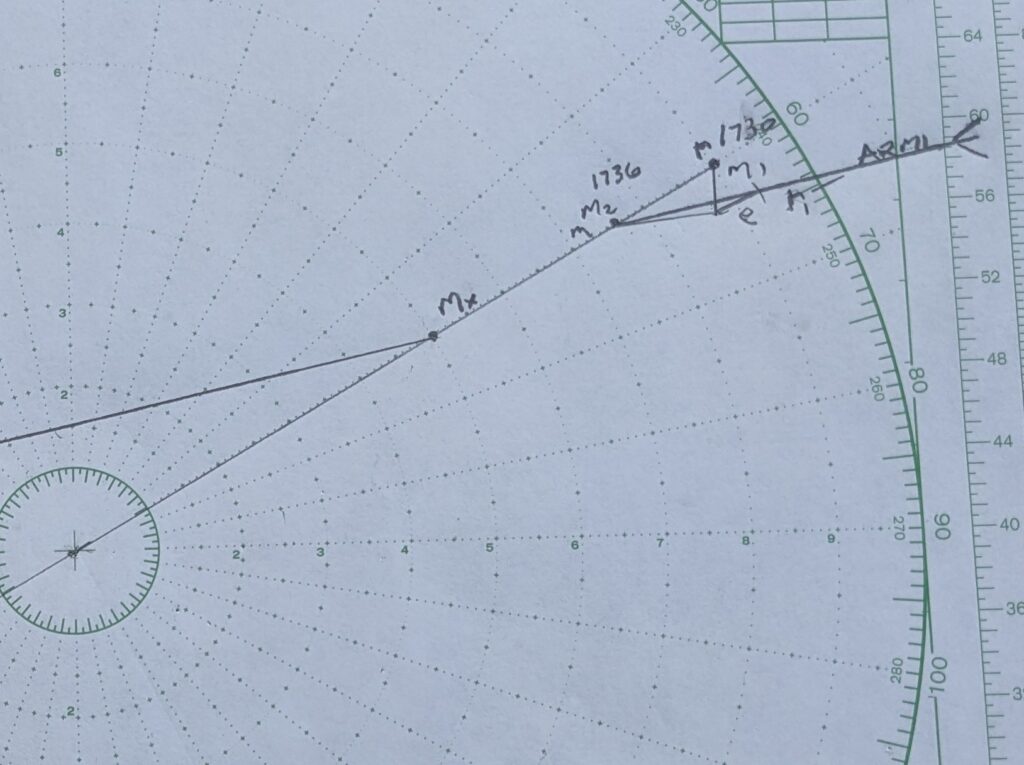
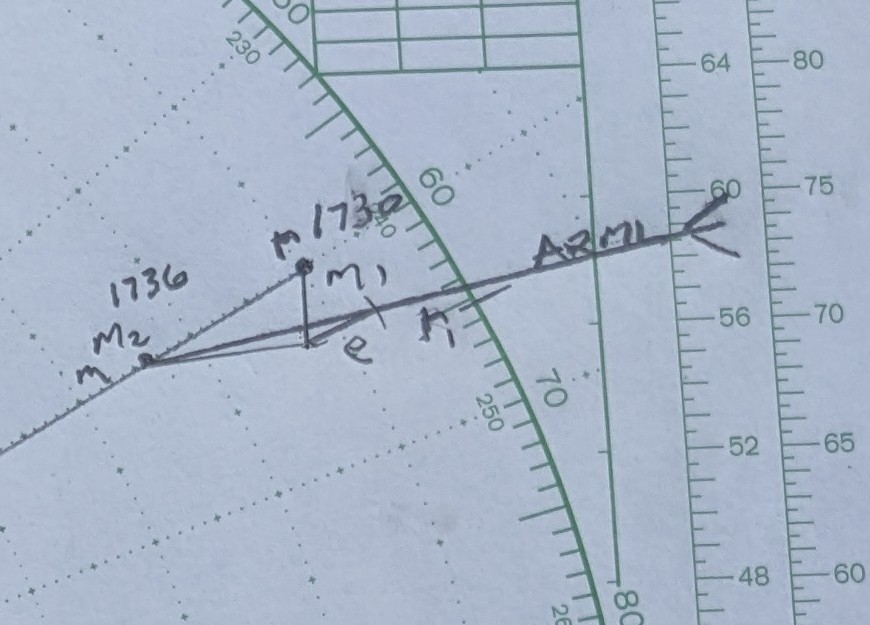
Start by indicating the spot to make your turn (M_x) at a range of 5 miles along the RML. Draw in a new relative motion line (NRML) beginning at M_x and just touching the 1.5 mile range ring.

Desired NRML with Mx at 5 miles
and 1.5 Mile CPA

Start by indicating the spot (M_x) to make your turn at a range of 5 miles along the RML. Draw in a new relative motion line (NRML) beginning at M_xand just touching the tangent of the 1.5 mile range ring.

The NRML here is 258R, and needs to be labeled.

Move, or advance, the NRML until it ends at point M₂. This new line becomes ARML.

ARML is parallel to NRML, ending at M2 on the plot.

Close up showing ARML and own ship course/speed arc.

Course to Steer

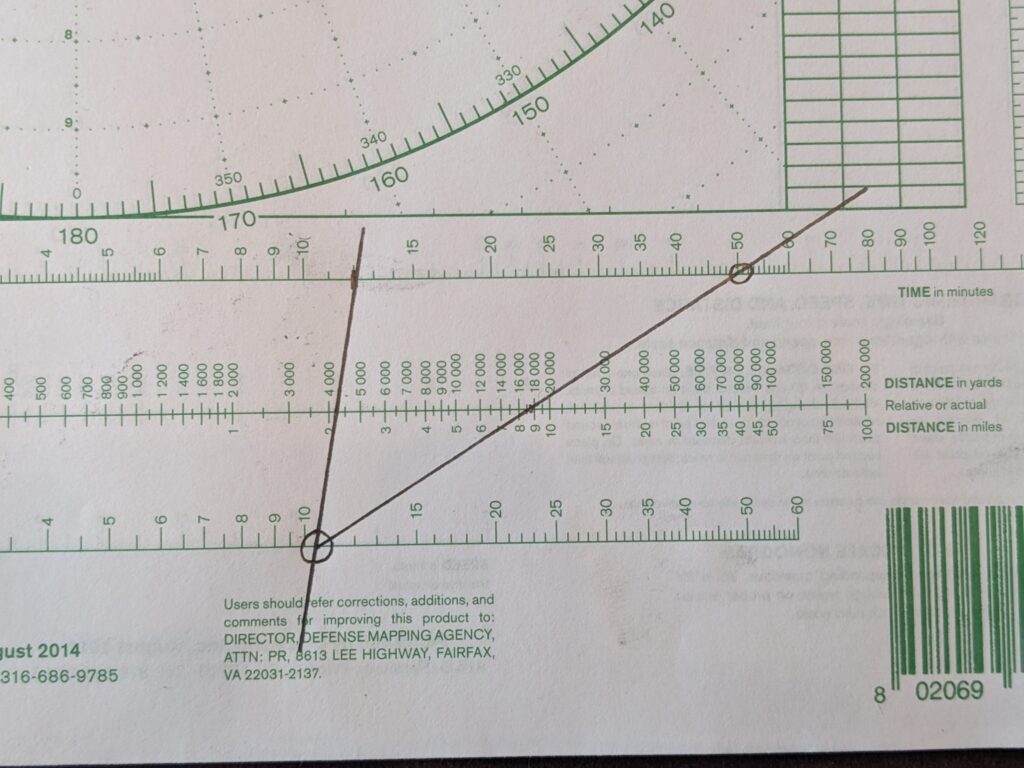
Set dividers to the distance of er (in this case, 6 miles) and strike an arc centered on e that intersects ARML. The intersection becomes r₁ (aka r prime).

Your new course to steer is 065. According to the original SRM, expect to arrive at M_x at 1747. On the new course, CPA will be 1.5 miles, 11 degrees off the port bow (349R), with a TCPA of 1803 (r₁m provides the a new SRM of 18 knots). Aspect will be red 102^∘ (nearly off the other vessel’s port beam).

A Second Method

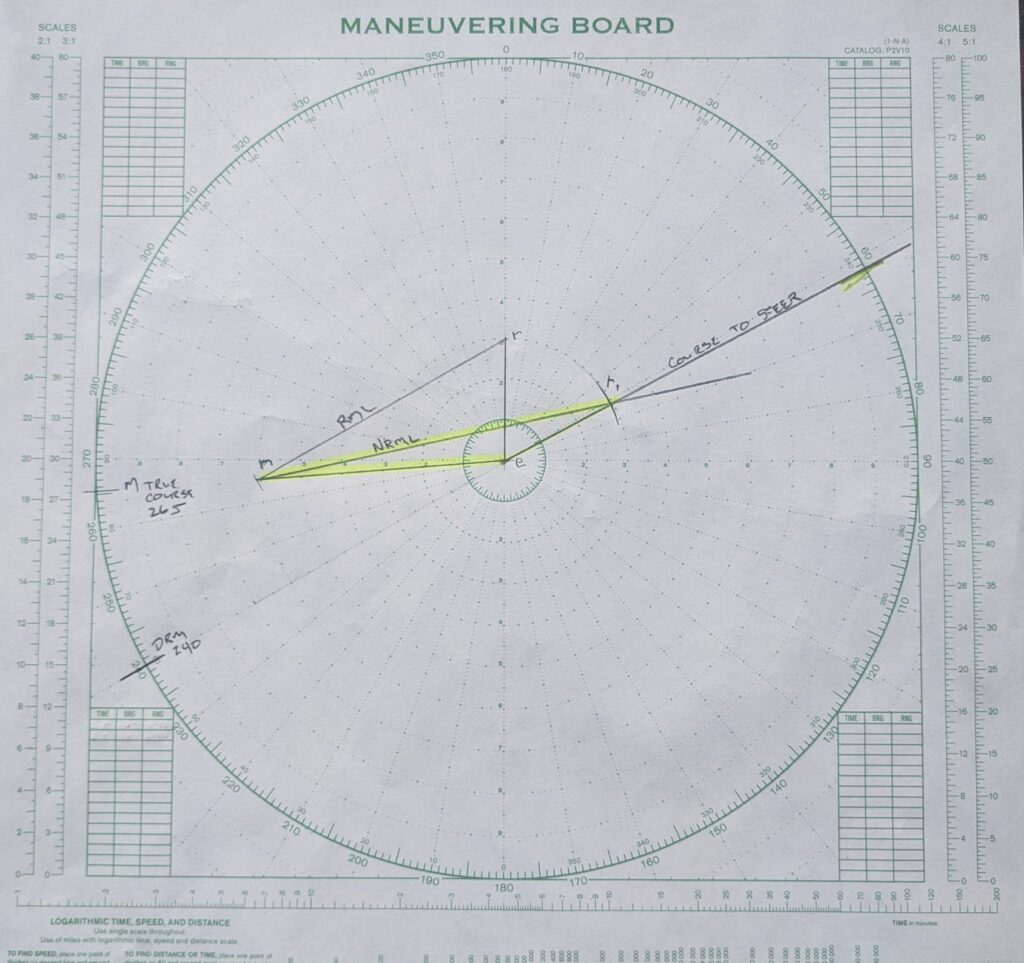
A second method of finding the same solution is available that many find more convenient as well as more accurate. Instead of completing the true course and speed and course to steer vector triangles using points M₁ and M₂, move them to the center of the mo board.

True Course and Speed Vector Triangle

One major difference exists. Instead of plotting “own ship” course to end at m, plot er beginning at the center and going in the direction of travel a distance equal to own ship speed. The RML line will then start at r and go towards m at a distance equal to SRM. “em” can now be added to the triangle. In the image, the unhighlighted pencil lines describe true course and speed vector triangle.

Course To Steer Vector Triangle

The course to steer vector triangle can now be completed. There is one constant between the true course and speed triangle and the course to steer triangle. Vessel M has a course of 265 and a speed of 12 knots. The em vector will not change. We also know NRML which was found using the original plot. Add the NRML to the plot, ending at m.

Set dividers to the distance of er and scribe an arc that crosses NRML. This is r prime. Your new course to steer is er₁ (062). In the image, the course to steer vector triangle has been highlighted in yellow.

You may notice, the first method gave a solution of 065 while the second method provided 062. A small difference which will be negligible in practice. I tend to prefer the second method because the size of the triangles tends to provide greater accuracy.
Course to Steer Problem Answers
February 1, 2023
Understanding the Maneuvering Board
Maneuvering Board Layout

The maneuvering board (aka mo board) is a diagram used in the solution of relative motion problems. In marine navigation there are several “problems” involving the use of relative vectors. As it pertains to marine navigation, relative vectors contain two factors, speed and direction.

Common problems encountered in navigation that are greatly simplified by the use of a mo board include:
- Relative wind to true wind calculations
- True wind to relative wind calculations
- Course to steer to avoid a storm
- Set and Drift
- Course to steer to overcome set and drift
- Relative motion of another vessel/object and its closest point of approach
- True course of another vessel
- Course to steer to avoid collision with another vessel/object
While all relative vector problems are plotted basically the same way, each problem has its own specific requirements such as labels. Therefore, each of these are discussed in full in individual lessons dedicated to the topics.

Parts of the Maneuvering Board

There are three main “parts” to the mo board.

Distance and Bearing Compass Rose

Most prominently displayed is a top down (polar) view consisting of equally spaced radial lines at 10^∘ intervals. An outer ring of numbers represents the points of a compass increasing in value in a clockwise direction from 0 at the top to 360. 1^∘ increments are found between each 10^∘ radial. An inner ring of numbers provides the reciprocal (180^∘ difference) value for each primary radial.

There are ten equal distant concentric circles, with each concentric circle subdivided by ten equally spaced dots. These concentric circles typically represent miles and tenths of a mile.

Scale

In the left-hand margin there are two vertical scales (2:1 and 3:1) and in the right-hand margin there are two vertical scales (4:1 and 5:1) to be used for easy conversion of distances up to 50 miles to the 10 ring distance scale in the rose.

Nomogram

A logarithmic time-speed-distance (TSD) scale and instructions for its use are printed at the bottom.

Using The TSD Nomogram

Three logarithmic scales are provided. Time in Minutes (0 to 200 minutes), Distance in Yards and/or Nautical Miles (25 to 200,000 yards) , and Speed in Knots (1 to 60 knots). Any two known quantities will provide a solution for the third with a simple line.

In the example below, another vessel has traveled 2.2 miles over a twelve minute time span. A line from 12 minutes on the top scale, drawn through the 2.2 mile value on the middle scale provides a speed of 11 knots.

That same vessel, will travel 8.8 miles over a 50 minute time period.

This example quickly calculated the relative speed of approach of another vessel, and the time required (50 min) to its closest point of approach.

Speed of Relative Motion and Time to CPA
February 1, 2023
Closest Point of Approach – CPA
Why?

The question of why use radar comes up often. Over the years, I have had a number of students who felt radar was outdated and of limited use in todays world of GPS, Chart Plotters, and AIS.

Sadly, this could not be further from the truth. One important point about radar’s value is its ability to tell at a glance how close you are to being on a collision course with an object. Whether another vessel, a buoy, or a rock, radar provides visual evidence of a target’s track in relation to you. Some simple plotting provides information about how close you will pass and how long you have before it happens.

Related Pages

Collision Avoidance

Bearings

Understanding the Maneuvering Board

Downloads

Maneuvering Board PDF

Radar Screen Orientation

The first thing to know is how your radar is set to display. Head Up, North Up, or Course Up. There are pro’s and con’s to each setting, and it really comes down to what your personal preference is.

Head Up

Head up always orients the screen to the direction your vessel is heading. Your direction of travel becomes 000. I see two main benefits to Head Up. First, all target echos are exactly relative to your vessel. Assuming clear visibility, if the screen paints a target at 090, all you need to do is look directly off the starboard beam. The target will be there. Second, when plotting own vessels course you will always plot directly on the 000/180 line (more on that in the Determining Other Vessel Course and Speed).

The disadvantage is an additional calculation when determining the other vessel’s true course. Again, more to come on that topic.

North Up

North Up uses a direction sensor to orient your screen to north. 000 on the screen will represent North, and a heading flasher (line) will appear to show your vessel’s heading. North Up takes a relative bearing and rotates it in such a way it is lined up with North. For example, if you are on a course of 045, a relative bearing of 090 degrees will paint on the screen at 135 degrees. Meaning that an object directly off the starboard beam may appear to be behind you while looking at the screen. On the other hand, using a compass oriented at 135 (don’t forget to adjust for variation) will point you in the direction of the object. While plotting your own course on the maneuvering board while in North Up mode, remember to plot using the direction of your heading, not the 000/180 line.

The primary advantage of North Up comes later, while calculating the other vessel’s true course.

Course Up

Course up is essentially the same as head up until you execute a turn. It will generally be treated in the same way as head up mode while calculating CPA and Time to CPA.

Head Up Example showing radar echo at 045 relative to your vessel’s heading. Image from Publication 1310, Radar Navigation and Maneuvering Board Manual, Seventh Addition 2001, page 36.

North Up Example showing radar echo at 315T, 045 relative to your vessel’s heading. Image from Publication 1310, Radar Navigation and Maneuvering Board Manual, Seventh Addition 2001, page 36.
Plotting Relative Contact Locations

Knowing your screen’s orientation is important, however, it does not impact the “how to” of finding CPA. Simply plot what you see on the screen. For the purpose of this discussion, we will be assuming exercises have the display set to head up.

Relative Bearings

As it pertains to radar, a relative bearing is always in relationship to your vessel’s heading, and progresses clockwise from 000° to 360°. Notation for a relative bearing is as follows: 045R is 45° clockwise of your vessel’s heading. 270R is 270° clockwise from the heading. A radar bearing is never cited as counter clockwise (left of) your current heading. A more complete discussion of True, Magnetic, and Relative bearings can be found in the Bearings lesson.

Relative Plot

To determine CPA, first create a relative plot showing the movement of your vessel vs the other vessel. A maneuvering board is a good tool for this task. An 8.5 x 11 inch pdf of a maneuvering board can be downloaded from the link at the top of the page. Various items within the plot must be labeled to prevent confusion and to help ensure success. There are a couple of different labeling methods in use. The one presented here is the one most commonly used. A second set of “vector triangle” labels used to identify relative to true vectors and course to steer vectors will be introduced later.

Relative Plot Labels
- R … Your Ship
- M … Other Ship
- M₁ … First Plotted Position of Other Ship
- M₂, M₃ … Later Plotted Positions of Other Ship
- M_x … Planned Position of Other ship at time of your maneuver to avoid
- Note: If more than one vessel is being tracked, replace M with another letter such as N, O, P, etc.
- RML … Relative Motion Line
- DRM … Direction of Relative Motion
- SRM … Speed of Relative Motion
- MRM … Miles of Relative Motion
- NRML … New Relative Motion Line
- CPA … Closest Point of Approach
Plotting the Target’s Location

When a target first appears on the radar, use the VRM and EBL tools to determine range and bearing. On a maneuvering board, plot the range and bearing of the target, as well as the time and a target identifier. In this case the target will be identified as “M”. The first plotted location will be identified as M₁.

Every plotted location has 4 data points:
1. Target “Name” (M, N, O …)
2. Time
3. Range
4. Bearing
Allow a period of time to elapse and use the VRM and EBL tools to capture the new range and bearing to the target. A common time lapse between plots is 6 minutes, although any convenient length of time may be used.

Plot this second location on the maneuvering board and label as M₂. While it’s desirable to have at least three plotted locations to ensure accuracy, two plotted locations can be used to begin an examination of the possibility of collision between you and the target.

6 Minute Rule

6 minutes is a standard time lapse between target plots because the distance traveled in 6 minutes is 1/10 of the speed. For example, if a vessel traveled .7 miles over 6 minute period of time that vessel speed is 7 knots.
RML (SRM & DRM)

Once you have two or more target locations plotted take a straight edge and draw a line beginning at M1 through M2 and continuing until you have gone past the center of the maneuvering board. Remember, that the center represents your vessel’s location.

This is your relative motion line and should be labeled RML. The direction of the RML in degrees is the direction of relative motion (DRM). It can be helpful to draw an arrow head at the end of the RML to remind you of the relative direction of travel between you and the other vessel. During later steps, it can be easy to confuse the DRM and use its reciprocal.

Measuring the distance between M₁ and M₂ provides the speed of relative motion (SRM). If you are using the 6 minute rule, simply multiply the distance traveled between M₁ and M₂ by 10. If any other time span is used, the nomogram at the bottom of the maneuvering board or “D Street” will assist in getting the correct speed.
The D STreet Triangle
If RML crosses directly through the center you are on a collision course. If it passes above or below the center, you are not and it’s time to calculate how close the vessel will be to you at its closest point of approach as well as what time that will happen.
An example
- M₁ at 0900 indicates a range of 9.0nm with a bearing of 274R
- M₂ at 0906, 8nm, 276R
- M₃ at 0912, 6.9nm 278R
RML with CPA and Heading Flash (dashed line from center to 000)

Speed of Relative Motion and Time to CPA

Once drawn, the RML is “moved” to the center and the bearing check against the compass scale. Other ship “M” has a DRM of 081R.

SRM is found by measuring the distance between any two plotted points along the RML. Two different ways to find the solution are provided. The measured distance from M₁ to M₂ is 1.1nm. Applying the 6 minute rule provides a SRM of 11 knots. In the image on the right, the nomogram is used to calculate SRM from M₁ to M₃, a distance of 2.2nm over 12 minutes. The top scale of the nomogram is time in minutes. The middle scale is distance in yards and/or miles. The bottom scale is speed. Drawing a line from 12 minutes thru 2.2 miles provides a speed solution of 11 knots.
Finding the CPA (Direction and Distance)

One the RML has been plotted it becomes easy to determine the closest point of approach distance, direction, and time. Scribe a line perpendicular to the RML from the center to find direction. The distance from the center to the RML provides distance. In the image above, CPA will be approximately 2nm at 352R (8^∘ to port looking over the bow).

Time to CPA (TCPA)

Time to CPA in the example is 48 minutes from point of first contact. It is a simple process to measure the distance from the plotted contact to the CPA. In this case, 8.8 miles from M₁ to CPA. Using the 11 knot relative speed calculated earlier, TCPA is 48 minutes (8.8 / 11 = .8 hours or 48 minutes). First contact was 0900. TCPA would be 0948.

Using the nomogram provides approximately the same answer as illustrated above.
Testing Your Skills

Here are two additional CPA problems. Plot the contacts and determine:
- DRM
- SRM
- Direction to CPA
- Distance to CPA
- TCPA
0908

0914

0920

040R

040R

040R

8.5 nm

7.3 nm

6.2 nm

Problem 1 Answer

1125

1131

1137

185R

184R

183R

7 nm

6.4 nm

5.8 nm

Problem 2 Answer
February 1, 2023